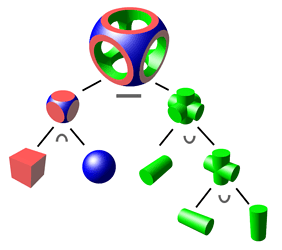
While I tend to prefer baking in the boolean operations we might perform in Rhino when I’m form modelling, say, replicating those steps across applications should be possible with a theoretical Base extension object of CSGSolid with a tree of operands and Solids. Rather like embedding the GH graph of boolean operations into an object type
Obviously, this would imply composition work in Applications that don’t natively support this representation, but in puristic terms, the Speckle paradigm could support this as a first-class Geometry type.
https://commons.wikimedia.org/w/index.php?curid=263170
In this archetypal diagram, each Base object could be structured and decoupled:
CSGSolid
↳ @Members: List<CSGSolid | Base>[]
↳ Operation: { Union | Difference | Intersection}
Alternatively,
CSGSolid
↳ Operations: List< Tuple< @Base, @Base, { Union, Difference, Intersection } >>[]
Without working through Psuedo# I’ve not gone into how terrible an implementation either is better. I like tree implied by the first, but if the transport of the second or even a simple array made sense then also gravy (e.g. [Base, Base, “union”, Base, Base, “intersection”]. The only caveat to this proposal is that the intermediary (component) objects don’t make a great deal of sense as visualised objects outside the context of the composite CSGSolid.
It just so happens that IFC, GeometryGym, Solidworks, FME, threejs & babylonjs do support it.
Solid isn’t directly a Speckle Geometry type to begin with, but that’s a different question 
Nevertheless, there isn’t really a restriction on there being one. It’s a tree of operations on anything valid really.
By extension a proposal for DonutSurfaces is implied 
